Q) Two pipes together can fill a tank in hours. The pipe with larger diameter takes 2 hours less than the pipe with smaller diameter to fill the tank separately. Find the time in which each pipe can fill the tank separately.

Ans:

VIDEO SOLUTION

STEP BY STEP SOLUTION

Method 1:

Let’s consider the volume of the tank is V Litres.

Next we consider the smaller pipe takes X hours to fill V litres , therefore it fills litres in 1 hr.

Next, larger pipe takes (X – 2) hours ti fill V litres, therefore it fills litres in 1 hr

Therefore, water filled by both the pipes together in 1 hr = litres

=  = litres

Next, since both pipes together fill litres in 1 hr

Hence, they will fill 1 litre in 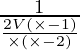hrs = hrs

Hence, they will fill V litres in = V x hrs = hrs

Next, since both pipes together fill the tank in hrs      (given)

hence,

8 X (X – 2) = 15 [ 2 (X – 1]

8 X² – 16 X = 30 X – 30

8X² – 46 X + 30 = 0

4 X² – 23 X + 15 = 0

4X² – 20 X – 3 X + 15 = 0

4X (X – 5) – 3(X – 5) = 0

(X – 5) (4 X – 3) = 0

X = 5 and X = –

Since x , therefore X = 5

and X – 2 = 3

Therefore, the pipe with larger diameter will take 3 hrs and smaller diameter pipe will take 5 hrs to fill the tank separately

Method 2: Let’s consider the smaller pipe takes X hours to fill the tank separately, therefore it fills tank in 1 hr.

Next, larger pipe takes X – 2 hours, therefore it fills tank in 1 hr

Therefore, tank filled by both the pipes together = …… (1)

Next, since both pipes together fill the tank in   hrs      (given)

hence, we can say, they together fill tank in 1 hrs. …… (2)

Next, by comparing equation (1) and (2), we get:

15 (2X – 2) = 8 X (X – 2)

30 X – 30 =  8 X² – 16 X

8X² – 46 X + 30 = 0

4 X² – 23 X + 15 = 0

4X² – 20 X – 3 X + 15 = 0

4X (X – 5) – 3(X – 5) = 0

(X – 5) (4 X – 3) = 0

X = 5 and X = –

Since x , therefore X = 5

and X – 2 = 3

Therefore, the pipe with larger diameter will take 3 hrs and smaller diameter pipe will take 5 hrs to fill the tank separately.

Please Press Heart Button, if you like the solution.