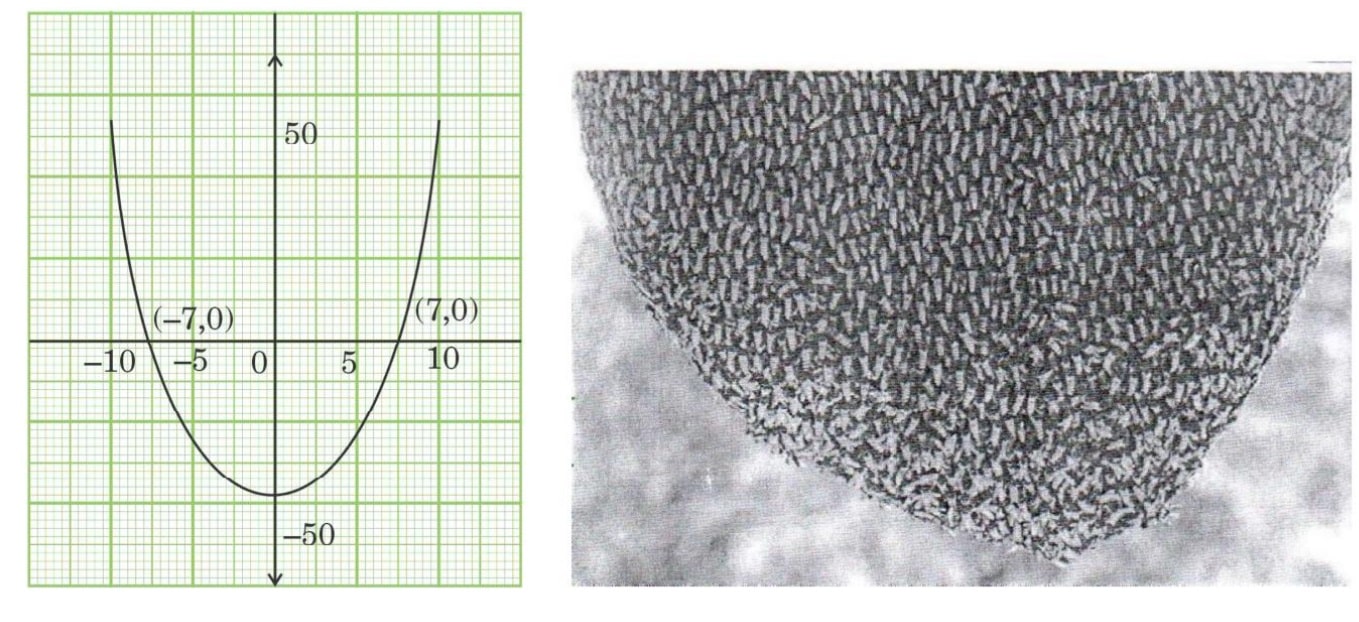
Q) While playing in a garden, Samaira saw a honeycomb and asked her mother what is that. Her mother replied that it’s a honeycomb made by honey bees to store honey. Also, she told her that the shape of the honeycomb formed is a mathematical structure. The mathematical representation of the honeycomb is shown in the graph.

Based on the above information, answer the following questions :
(i) How many zeroes are there for the polynomial represented by the graph given ?
(ii) Write the zeroes of the polynomial.
(iii) (a) If the zeroes of a polynomial x² + (a + 1) x + b are 2 and – 3, then determine the values of a and b.
OR (iii) (b) If the square of difference of the zeroes of the polynomial x² + px + 45 is 144, then find the value of p.

Ans:

(i) zeroes of the polynomial:

We know that the zeroes are represented based on no. of times, the graph cuts the X- axis.

Here in the given diagram, Polynomial graph cuts X-Axis 2 times,

Therefore there are 2 zeroes.

(ii) Zeroes of the polynomial:

Here, Polynomial cuts the X-axis at (7, 0) and (-7,0)

Hence, value of X are 7 and – 7

Therefore, zeroes of the polynomial are 7 and – 7.

(iii) (a) Value of a and B:

Polynomial given, f(x) = x ² + (a + 1) x + b

By writing the given polynomial, f(x) = 0, we get:

x²  + (a + 1) x + b = 0

Next, comparing it with standard quadratic equation, A x ²  + B x + C = 0

we get, A = 1, B = (a + 1), C = b

We know that, Sum of the roots, α + β =

Since, Zeroes are given as 2, -3,

hence for given polynomial, Sum of the roots:

(2) + (- 3) =

∴ – 1 = – (a + 1)

∴ – 1 = – a – 1

∴ a = 0

Next, Product of the roots, α . β =

Hence, for given polynomial, product of the roots:

2 (- 3) =

∴ – 6 = b

∴ b = – 6

Therefore, values of a and b are 0 and – 6, respectively.

(iii) (b) Value of p:

Given the polynomial: f(x) = x²  + px + 45

By writing the given polynomial, f(x) = 0, we get:

x²  + p x + 45 = 0

Next, comparing it with standard quadratic equation, A x ²  + B x + C = 0

we get, A = 1, B = p, C = 45

We know that, Sum of the roots, α + β =

hence, if zeroes are α & β, then (α + β) =

∴ (α + β) = – p ……….. (i)

Next, Product of the roots, α . β =

Hence, for given polynomial, product of the roots:

α . β =

∴ α β = 45

∴ α = ……….. (ii)

Also, we are given that square of difference of the zeroes = 144

∴ (α – β) ² = 144

∴ (α – β) ² = (12)²

∴ (α – β) = 12 ………. (iii)

By substituting value of α from equation (ii) one by one, we get:

(α – β) = 12

∴ ( – β) = 12

∴ (45 – β² ) = 12 β

∴ β² + 12 β – 45 = 0

∴ β² + 15 β – 3 β – 45 = 0

∴ β (β + 15) – 3 (β + 15) = 0

∴ (β + 15) (β – 3) = 0

∴ β = 3, β = – 15

Case 1, when β = 3,

α =

∴ α = View Post

∴ α = 15

Hence, α = 15 and β = 3

Now from equation (i),

(α + β) = – p

By substituting values of α & β, we get

15 + 3 = – p

∴ p = – 18

Case 2, when β = – 15,

α =

∴ α = – 3

Hence, α = – 3 and β = – 15

Now from equation (i),

(α + β) = – p

By substituting values of α & β, we get

– 3 + (- 15) = = p

∴ p = – 18

Therefore, in both cases, value of p is – 18.

Please do press “Heart” button if you liked the solution.