Q) Solve the following system of equations graphically: x – y + 2 = 0 and 4 x – y – 4 = 0. Calculate the area of the triangle formed by the lines so drawn and x – axis.

(Q 34 – 30/1/3 – CBSE 2026 Question Paper)

Part 1: Solving the linear equations:

Step 1: To plot the equations, let’s first find out the coordinates of points lying on these lines:

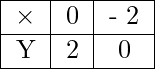
For line: x – y + 2 = 0, we calculate coordinates of various points:

at X = 0, (0) – y + 2 = 0 => y = 2 ∴ Point is (0, 2)

at Y =0, x – (0) + 2 = 0 => x = – 2 ∴ Point is (- 2, 0)

Hence, we get the following table:

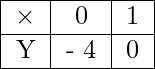
Step 2: Similarly, for line: 4 x – y – 4 = 0, we calculate coordinates of various points:

at X = 0, 4(0) – y – 4 = 0 => y = – 4 ∴ Point is (0, – 4)

at Y =0, 4 x – (0) – 4 = 0 => x = 1 ∴ Point is (1, 0)

Hence, we get the following table:

Step 3: Now let’s plot both of these lines connecting each of the points:

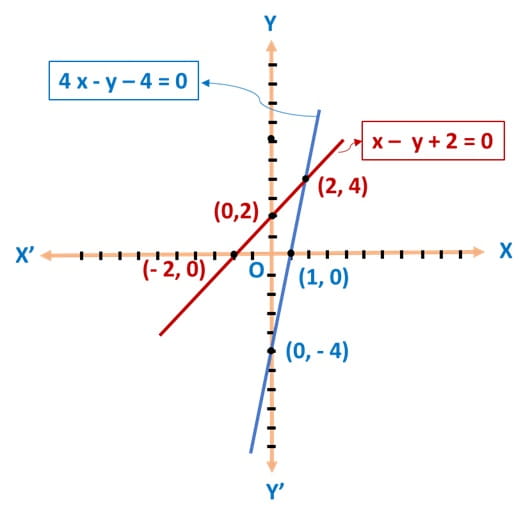
From the diagram, we can see that the lines intersect each other at point (2, 4)

Therefore, the solution of the lines is (2, 4).

Part 2: Area of the triangle formed by two lines and X axis:

Step 4: x – y – 2 = 0 cuts X – axis at (- 2, 0)

and 4 x – y – 4 = 0 cuts X- axis at (1, 0)

Both lines intersect each other at (2, 4)

Hence, the 3 points of the triangle are: A (- 2,0), B (1, 0) and C (2,4)

Step 5: From the diagram: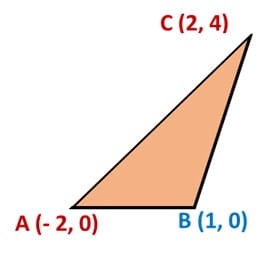

Base of the triangle

= Distance of abscissa of A & B

= 1 – (- 2) = 3 units

Height of the triangle

= ordinate value of point C (2,4)

= 4 units

∴ Area of the triangle = x Base x Height

= x 3 x 4 = 6 sq units

Therefore, the area of the triangle between lines & X-axis is 6 sq. units.

Please press the “Heart”, if you liked the solution.