Q) ABCD is a rectangle formed by the points A (−1, −1), B (−1, 6), C (3, 6) and D (3, −1). P, Q, R and S are mid-points of sides AB, BC, CD and DA respectively. Show that diagonals of the quadrilateral PQRS bisect each other.
Ans: Let’s make a diagram for the given question:
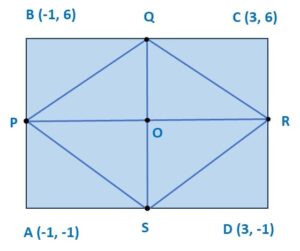
Let’s start fiding coordinates of points P, Q, R and S.
We know that the coordinates of a midpoint lying between (x1, y1) and (x2, y2) is given by:
M(x,y) = ![]()
Since P is the midpoint of AB, ∴ P = ![]() = (- 1,
= (- 1, ![]() )
)
Similarly, Q is the midpoint of BC, ∴ P = ![]() = (1, 6)
= (1, 6)
Similarly, R is the midpoint of CD, ∴ P = ![]() = (3,
= (3, ![]() )
)
Similarly, S is the midpoint of DA, ∴ P = ![]() = (1, – 1)
= (1, – 1)
If Diagonals of PQRS bisect each other, O will be the midpoint of PR and QS both.
Let’s check if this relationship is verified:
If O is the midpoint of PR, then its coordinates are given by: ![]() = (1,
= (1,![]() )
)
If O is the midpoint of QS, then its coordinates are given by: ![]() = (1,
= (1,![]() )
)
Since both points coordinates match with each other, it confirms that O is midpoint of PR & QS
Therefore, diagonals of quadrilateral PQRS bisect each other.
Please press the heart button, if you liked the solution.
