Q) Find the area of the shaded region in Figure, where arcs drawn with centres A, B, C and D intersect in pairs at mid-points P, Q, R and S of the sides AB, BC, CD and DA respectively of a square ABCD. (Use π = 22/7)
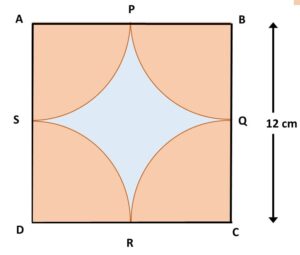
Ans: We are given that an arc is drawn at each corner of the square.
Also it is given that the arcs from adjacent vertices are meeting at a point which is a mid point of the side i.e.
∵ P is the midpoint of AB; ∴ So, AP = PB = ![]() = 6 cm
= 6 cm
Here, 14 cm is the side of the square. hence, Arc’s radius = 6 cm
Similarly, Q is the midpoint of BC, ∴ BQ = QC = ![]() = 6 cm
= 6 cm
R is the midpoint of CD, ∴ CR = DR = 12/2 = ![]() = 6 cm
= 6 cm
S is the midpoint of DA, ∴ AS = SD = 12/2 = ![]() = 6 cm
= 6 cm
Now, the area of shaded region = Area of square – 4 x Area of the quarter circles
= (S)2 – 4 x ![]()
= (S)2 – ![]()
= (12)2 – ![]()
= 144 – 113.04 = 30.96 cm2
Therefore, the area of unshaded region in the center is 30.96 cm2.
