Q) In the given figure, tangents PQ and PR are drawn to a circle such that ∠RPQ = 300. A chord RS is drawn parallel to tangent PQ. Find the ∠RQS.
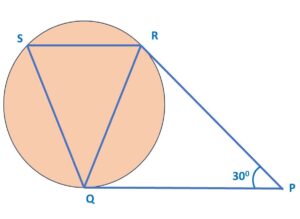
Ans: In △PRQ, PQ and PR are tangents from an external point P to circle.
∴ PR = PQ
Since the angles opposites to equal sides are equal
∴ ∠PRQ = ∠PQR
Now, by Angle sum property, in △PRQ, ∠PRQ + ∠PQR + ∠RPQ = 1800
∵ ∠RPQ = 300
∴ ∠PRQ + ∠PRQ + 300 = 1800
∴ 2 ∠PRQ + 300 = 1800
∴ ∠PRQ = 750
Therefore, ∠PRQ= ∠PQR = 750
Since PQ ∥ SR, and RQ cuts these 2 lines:
∴ ∠PQR = ∠SRQ = 750 (Alternate angles)
Since PQ is tangent at Q and QR is chord at Q.
∴ ∠RSQ = ∠PQR = 750 (∠RSQ in alternate segment of circle]
Now, In △SRQ,
∵ ∠RSQ + ∠SRQ + ∠SQR = 1800 (Angle sum property of a triangle)
∴ 750 + 750 + ∠SQR = 1800
∴ ∠SQR = 1800 – 1500
∴ ∠SQR = 300
