Q) The vertices of Δ ABC are A (- 2, 4), B(4, 3) and C(1, – 6). Find length of the median BD.

Ans: Let’s plot the points on the graph:

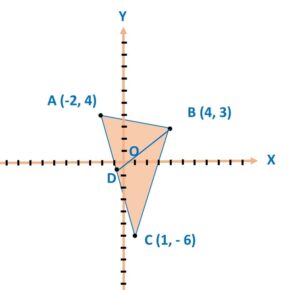
Step 1:  To draw median BD, point D lies on AC

Let’s consider the coordinates of D are (X, Y)

Since D is the midpoint of A C, we need to find out the coordinates of D.

We know that the coordinates of mid point of 2 coordinates (X₁, Y₁) and (X₂, Y₂) given by:

(X, Y) =

∴ Value of coordinates of midpoint D of A (- 2, 4) and C (1, – 6) are:

(X, Y) =

=

Step 2: Next, we find length of BD, where B is (4, 3) and D is (

We know that the distance between two points (X₁, Y₁) and (X₂, Y₂) is given by:

S = √ [(X₂ – X₁)² + (Y₂ – Y₁)^{2 ]}

∴  BD =

=

=

= 6.02

Therefore, the length of the median BD is 6.02 units.

Please press the “Heart”, if you liked the solution.