Q) Two pillars are standing on either side of a 80 m wide road. Height of one pillar is 20 m more than the height of the other pillar. From a point on the road between the pillars, the angle of elevation of the higher pillar is 60°, whereas that of the other pillar is 30°. Find the position of the point between the pillars and the height of each pillar. (Use √3 = 1.73)

Ans:

Let’s start from the diagram for the question:

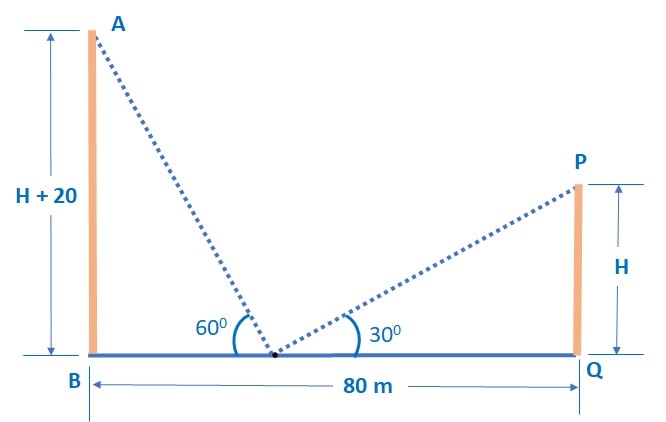
Let ‘s take AB as higher pillar and PQ as a smaller pillar with the height as ‘H’.

∴ height of higher pillar AB = H + 20 m

Let the point on the road be R and distance BR be X

∴ distance RQ = 80 – X

Let’s start from In Δ ABP, tan R =

Since, ∠ ARB = 60⁰ , AB = H + 20, BP = X

∴ tan 60⁰ = √3 =

∴ X = …………. (i)

(Note: Here we calculate X in terms of H, because when we substitute value of X, we will get all H terms together and value of H will be calculated.)

Next, in Δ PRQ, tan R =

Since, ∠ PRQ = 30⁰ , PQ = H, RQ = 80 – X

∴ tan 30⁰ =

∴ 80 – X = H √3 …………. (ii)

By substituting, value of x from equation (i) in equation (ii), we get:

80 –   = H √3

∴ 80 √3 – ( H + 20) = 3 H

∴ 80 √3 – 20 = 4 H

∴ H = 20√3 – 5 = 20 x 1.73  – 5 = 29.6 m

Therefore the height of the smaller pillar is 29.6 m

Height of the higher pillar AB = H + 20

= 29.6 + 20 = 49.6 m

Therefore, the height of the higher pillar is 49.6 m

From equation (ii),

80 – X = H √3

We calculated above that, H = 20√3 – 5

∴ 80 – X = (20√3 – 5 ) √3 =  60  – 5 √3

X = 20 + 5 √3  = 20 + 5 x 1.73 = 28.65 m

Therefore, the distance of the point R from higher pillar is 28.65 m

Next, the distance of the point R from smaller pillar:

RQ = 80 – X = 80 – 28.65 = 51.35 m

Therefore, the distance of the point R from smaller pillar is 51.35 m